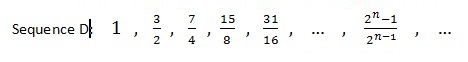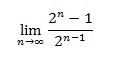Summary:
- An Infinite Sequence is just a long (infinite) list of numbers!
- A sequence converges if the numbers at the end are all essentially the same
- A sequence diverges if the numbers at the end go to infinity, or if they oscillate between different numbers
- You should take a Limit in order to see what the numbers at the end look like
- An Infinite Sequence is just a long (infinite) list of numbers!
- A sequence converges if the numbers at the end are all essentially the same
- A sequence diverges if the numbers at the end go to infinity, or if they oscillate between different numbers
- You should take a Limit in order to see what the numbers at the end look like
< back to Selected Math Topics >
The Math Tutor - Austin
Infinite Sequences - Easier than you think!
An Infinite Sequence is just a list of numbers!
Seriously - there's nothing special going on here! A "sequence" is just a list of numbers in a particular order, and an "infinite sequence" is just a list which keeps on going forever...
Here's one example of an infinite sequence:
Example:
Sequence "A" : 1, 2, 3, 4, 5, 6, 7, 8, 9, ...
(Note how I cleverly used the "..." to show how the sequence kept going on and on, even though I was too lazy to write it all)
One problem with infinite sequences, of course, is that they're - well - infinite! And of course, that means that I can't write out the whole thing even if I want to! Instead, I have to rely on you knowing what numbers should follow after the "9". (You do know, don't you? ;) )
It can help to have a formula to figure out which numbers come next...
Of course, figuring out what numbers come next can be a bit of an issue.
For example, this one might not be too bad:
Example:
Sequence "B" : 1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, ... (What numbers should come after "1/7" ?)
But - this next one might be a little tougher:
Example:
Sequence "C" : 2, 1, 1/2, 1/4, 1/8, 1/16, 1/32, ...
(If you haven't seen something like this before, you might miss the fact that each number is half of the one that comes before it in the list)
In this case, it would be a lot easier if we had a formula to help tell us which numbers should come next. Of course - this formula needs to know where we are in the list. (In most cases, when people write a formula for the series, they will use a letter like "n" or "m" or "k" to stand for where we are in the list).
For example, if we looked at Sequence "B" above, I'm thinking we could use the formula "1/n" to generate all of the numbers in the sequence. Here's how it works:
Example:
Generate all of the numbers in the sequence whose formula is "1/n":
The first item (n=1):
Because this is the first number in the list, we should use "1" in place of n in our formula
1/n = 1/1 = 1
The second item (n=2):
Because this is the second item, we should use "2" in place of n:
1/n = 1/2
The third item (n=3):
(I hope you're getting the picture - we should use "3" in place of n)
1/n = 1/3
Putting that all together, and writing our answers one after the other, we get:
1, 1/2, 1/3, ...
Since the list we get using the formula "1/n" matches the original list for Sequence B, we could use that formula to help describe the sequence:
Sequence "B" : 1, 1/2, 1/3, 1/4, 1/5, 1/6, ... , 1/n, ...
Because a formula helps so much to describe all of the numbers in the sequence, sometimes people will just give you the formula instead of writing out the sequence at all. If that happens, don't panic! Just remember that the formula is there only to help you calculate which numbers belong in the infinite sequence.
Example:
The sequence given by (2n+1)/(n+1) can be written explicitly as:
3/2, 5/3, 7/4, 9/5, ...
It can also help to know where the sequence is going!!
Sequences show up in real life as trends - and it'd be a good idea to know where the trend is going.
For example, assuming you lived forever, the daily balances in your bank account would be an infinite list of numbers (i.e., an infinite sequence).
Now, if those balances looked like this:
$100, $102, $104, $106, $108, ...
then you ought to be fairly happy - it's going up every day, and if you wait long enough, you could have an unlimited amount saved! (Mathematicians like to say "the trend is going to infinity")
On the other hand, if your daily balances looked like this:
$100, $50, $25, $12.50, $6.25, ...
then you might get a little worried. The balances are going down every day, and pretty soon you'll have no money left!
(Mathematicians like to say "the trend is going to zero")
But what about more complicated sequences?
For example, suppose we needed to figure out the trend for a sequence like this:
Well, here I'd say our best clue is the formula. As we go further and further down the list, we keep plugging bigger and bigger numbers in for "n". Perhaps, when we get really far along (i.e, as "n" goes to infinity), these numbers might get closer and closer to a limit...
But hey - this is calculus! If we're looking for a limit, we can just go ahead and calculate it!
And there you go - the formula above gets closer to "2" as "n" goes off to infinity. This means that, eventually, the numbers in our list get closer and closer to the number "2".
Convergence and Divergence
Convergence and Divergence are just terms used to describe how the trend in any given sequence behaves.
- if the numbers in the sequence go to a limit, (and not to infinity), then the sequence converges.
- if the numbers in the sequence go to infinity, then the sequence diverges
- if the numbers in the sequence don't settle down to one number, then the sequence also diverges
Convergence and Divergence
Convergence and Divergence are just terms used to describe how the trend in any given sequence behaves.
- if the numbers in the sequence go to a limit, (and not to infinity), then the sequence converges.
- if the numbers in the sequence go to infinity, then the sequence diverges
- if the numbers in the sequence don't settle down to one number, then the sequence also diverges